Matematicas

TEMAS TRABAJADOS EL PRIMER PERIODO.

1. POTENCIACIÓN:  La potenciación es una operación matemática entre dos términos denominados: base a y exponente n. Se escribe aⁿ  . 

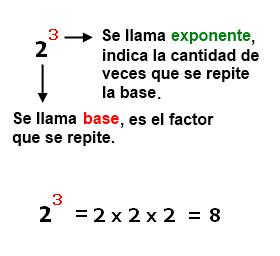
                EJEMPLOS DE POTECIACIÓN:

                 PROPIEDAD 1:

                

               4°= Siempre Que el exponente Sea 0 el resultado es 1

              

                 PROPIEDAD 2:

                0°=Siempre que la base es 0 y el exponente 0 el resultado va se indeterminado

                PROPIEDAD 3:

                a 1 =Siempre que  tenga potencia 1 es igual a la misma base 

             TABLAS DE MUTIPLICAR

Tabla de multiplicar

Tabla del 1 1 × 0 = 0 1 × 1 = 1 1 × 2 = 2 1 × 3 = 3 1 × 4 = 4 1 × 5 = 5 1 × 6 = 6 1 × 7 = 7 1 × 8 = 8 1 × 9 = 9 1 × 10 = 10 1 × 11 = 11 1 × 12 = 12	Tabla del 2 2 × 0 = 0 2 × 1 = 2 2 × 2 = 4 2 × 3 = 6 2 × 4 = 8 2 × 5 = 10 2 × 6 = 12 2 × 7 = 14 2 × 8 = 16 2 × 9 = 18 2 × 10 = 20 2 × 11 = 22 2 × 12 = 24	Tabla del 3 3 × 0 = 0 3 × 1 = 3 3 × 2 = 6 3 × 3 = 9 3 × 4 = 12 3 × 5 = 15 3 × 6 = 18 3 × 7 = 21 3 × 8 = 24 3 × 9 = 27 3 × 10 = 30 3 × 11 = 33 3 × 12 = 36	Tabla del 4 4 × 0 = 0 4 × 1 = 4 4 × 2 = 8 4 × 3 = 12 4 × 4 = 16 4 × 5 = 20 4 × 6 = 24 4 × 7 = 28 4 × 8 = 32 4 × 9 = 36 4 × 10 = 40 4 × 11 = 44 4 × 12 = 48	Tabla del 5 5 × 0 = 0 5 × 1 = 5 5 × 2 = 10 5 × 3 = 15 5 × 4 = 20 5 × 5 = 25 5 × 6 = 30 5 × 7 = 35 5 × 8 = 40 5 × 9 = 45 5 × 10 = 50 5 × 11 = 55 5 × 12 = 60
Tabla del 6 6 × 0 = 0 6 × 1 = 6 6 × 2 = 12 6 × 3 = 18 6 × 4 = 24 6 × 5 = 30 6 × 6 = 36 6 × 7 = 42 6 × 8 = 48 6 × 9 = 54 6 × 10 = 60 6 × 11 = 66 6 × 12 = 72	Tabla del 7 7 × 0 = 0 7 × 1 = 7 7 × 2 = 14 7 × 3 = 21 7 × 4 = 28 7 × 5 = 35 7 × 6 = 42 7 × 7 = 49 7 × 8 = 56 7 × 9 = 63 7 × 10 = 70 7 × 11 = 77 7 × 12 = 84	Tabla del 8 8 × 0 = 0 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 8 × 6 = 48 8 × 7 = 56 8 × 8 = 64 8 × 9 = 72 8 × 10 = 80 8 × 11 = 88 8 × 12 = 96	Tabla del 9 9 × 0 = 0 9 × 1 = 9 9 × 2 = 18 9 × 3 = 27 9 × 4 = 36 9 × 5 = 45 9 × 6 = 54 9 × 7 = 63 9 × 8 = 72 9 × 9 = 81 9 × 10 = 90 9 × 11 = 99 9 × 12 = 108	Tabla del 10 10 × 0 = 0 10 × 1 = 10 10 × 2 = 20 10 × 3 = 30 10 × 4 = 40 10 × 5 = 50 10 × 6 = 60 10 × 7 = 70 10 × 8 = 80 10 × 9 = 90 10 × 10 = 100 10 × 11 = 110 10 × 12 = 120

                                 TEMAS TRABAJADOS EL SEGUNDO PERIODO.
 

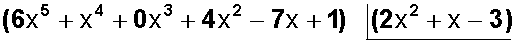
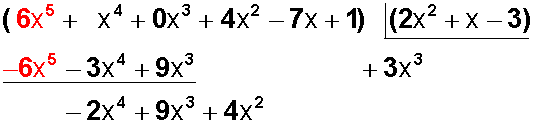
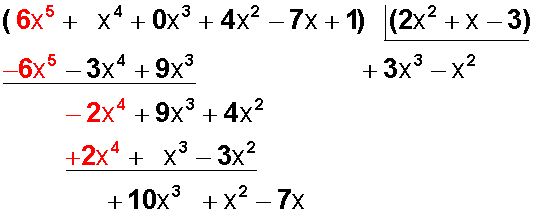
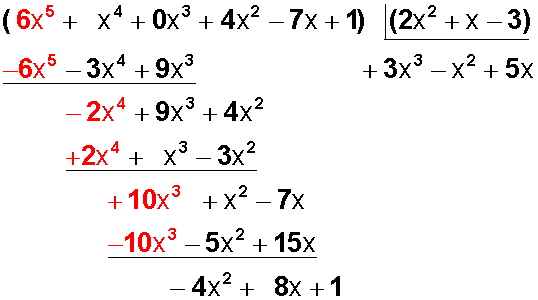
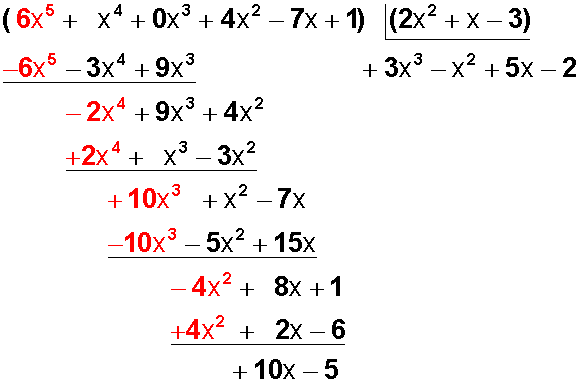
1.           .MONOMIOS Y POLINOMIOS:

   

• MONOMIO:Expresion algebraica que consta de un solo numero, una sola variable un solo exponente, un solo radical.  2a²bc³ − 5a²bc³ + 3a²bc³ − 2 a²bc³
• POLINOMIO:Expresion algebraica compuestos por 2 o mas monomios. 

       Cada expresion algebraica tiene un nombre:
     Monomio
      Binomio
     Trinomio
     Polinomio
                       
        PROPUESTAS DE LA COMO SE VA DESARROLAR LA CLASE DE ALGEBRA.

     1. Llegada puntual a clase
     2.Comportamiento
     3.presentacion puntual.

•       NOTACION ALGEBRAICA

      Los simbolos usados en algebra para representar las cantidades de las letras del abecedario .Los numeros se emplean para representar cantidades conocidas y determinadas, las letras se emplean para representar toda clase de cantidades conocidas y desconocidas ,las cantidadedes conocidas se expresan por las primeras letras del abecedario
             a,b,c,d,e
Las cantidades esconocidas se representas por las ultimas letras del abecedario
            u,w,x,y,z

•    TERMINO ALGEBRAICO:sSon expresiones matematicas que distinguen dos componenetes , un "coeficiente" (factor numeral) y un "factor literal" Compuesta de una a mas letras con sus respectivos componentes un termino consta;                                                                                    a.El signo: + o -                                                                                                                                b.Coeficiente Numerico 15,30,1                                                                                                                                                       2                                                                                                      c.Factor literal:  ab a la 3, x a la 4.
• GRADO DE UNA EXPRESION ALGEBRAICA:                                                                TERMINO: El grado de un termino  se calcula sumando los exponentes de la parte literal                Ejemplo:  a b a la 3  de 4 por que  1 +3:4      .                                                                                
•     EXPRESION ALGEBRAICA:                                                                                                       Monomios : cuando tiene un solo termino                                                                                       Binomios :cuando tiene dos terminos                                                                                             Trimonio : cuando tienen 3 terminos                                                                                               Polinomios:es el que tiene 4 o mas numeros                                                                                           
• TERMINOS SEMEJANTES:Son aquellos que tienen el mismo factor literal (mismas letras con los mismos exponentes). los terminos semejantes se pueden sumar o restar sumando o restando sus coeficientes numerico o conservan el factor literal                                                                       
• SUMA Y RESTA DE POLINOMIOS :La suma o resta de dos o mas polinomios da como el resultado de otro polinomio formado por la suma o la diferencia, en cada polinomio.cuando hay termino semejantes, hacemos reduccion de tales terminos .                                                          Ejemplo. SUMA:     Ejemplos .Resta. 
• MULTIPLICACION DE EXPRESIONES ALGEBRAICAS.                                                         LOGRO:Realizar multiplicaciones entre monomios y polinomios, para multiplicar monomios entre si los coeficientes numericos, luego se suman los exponentes de las letras semejantes.          
• MULTIPLICACION DE UN POLINOMIO POR UN MONOMIO.                                             Para multiplicar un polinomio por un monomio  se multiplica el monomio por cada uno de los terminos del polinomio se multiplica asi 
• MULTIPLICACION DE POLINOMIOS.                                                                                        se  multiplica cada monomio del primer polinomos por todos los elementos del segundo polinomio se suman los monomios  se suman del mismo grado                                                      *Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios se multiplica                                                                                                                                                                                                                                                                                                  Consulta 
• Productos notables  que es , Ejemplos                                                                                                                                                 Solucion                                                                                                1.Productos notables : Cada producto notable corresponde de una formula de fasctorizacion por ejemplo , la factorizacion de una diferencia de cuadrados perfecto es un producto de dos binomios conjugados y reciprocamente.                                                              Ejemplos  
• Binomio al cuadrado 
• suma por diferencia
• binomio al cubo
• trinomio al cuadrado
• suma de cubos
• diferencia de cubos
• productos de dos binomios que tienen en comun                                                                                              
• BINOMIO AL CUADRADO: Un binomio al cuadrado es una suma algebraica que se suma por sí misma, es decir, si tenemos el binomio a + b, el cuadrado de ese binomio es (a + b) (a + b) y se expresa como (a + b)2.                                              
• CUBO DE UN BINOMIO:Es igual a la primera cantidad elevada a un cubo mas el triple producto de la primera cantidad al cuadrado al segundo mas el el triple producto  elevada al cuadrado mas segunda cantidad elevada al cubo. Repaso de todos los temas visto Para una evalucacion el 18 de agosto del 2017

                       
                                        TEMAS TRABAJADOS EL TERCER PERIODO


DIVISION DE POLINOMIOS

Por definición, sabemos que un polinomio está formado por la suma o resta de varios monomios.

Un polinomio se puede dividir por un monomio o por otro polinomio.

La operación es muy similar a la división tradicional de números, donde hay un divisor, un dividendo, un cociente y un resto.

Dividir un polinomio se ve más complejo por la inclusión de términos algebraicos que tienen letras y números.

Por ello, para explicar la división de polinomios desarrollaremos un ejercicio práctico:

Vamos a dividir el polinomio

(6x 5 + x 4 + 4x 2 – 7x + 1) entre (2x 2 + x – 3)

Primero, ordenamos tanto el dividendo como el divisor de mayor a menor según sus grados, y completamos el grado que falte:

(6x 5 + x 4 + 0x 3 + 4x 2 – 7x + 1) entre (2x 2 + x – 3)

En el dividendo agregamos 0x 3 ya que ese grado faltaba.

Ahora, el polinomio, que es el dividendo, lo colocamos a la izquierda, y el divisor lo ponemos enmarcado a la derecha:

Dividimos el primer monomio del dividendo (+6x 5 ) entre el primer monomio del divisor (+2x 2 ).

+6x 5 : +2x 2 = +3x 3

Este resultado (+3x 3 ) lo ponemos debajo de la caja y lo multiplicamos por cada término del polinomio divisor y el resultado lo vamos restando en el polinomio dividendo:

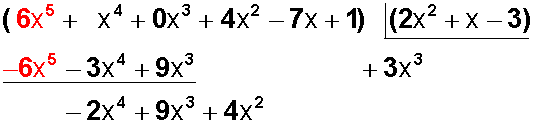
Aquí debemos tener cuidado: al multiplicar  +3x 3 , primero por +2x 2 ; luego por + x y luego por -3, hay que tener en cuenta la regla de los signos, y el resultado que pongamos abajo en el dividendo debe llevar signo contrario al obtenido.

Bajamos el monomio siguiente (+4x 2 ) y continuamos:

Ahora dividimos -2x 4 : +2x 2 = -x 2

Y este resultado lo agregamos al cociente y lo multiplicamos por +2x 2 , luego por +x y luego por -3:

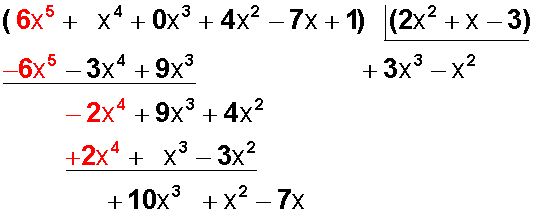
Bajamos e monomio siguiente (-7x),

y ahora dividimos +10x 3 : + 2x 2 = + 5x

Y +5 x lo agregamos  al cociente, lo multiplicamos por +2x 2 , luego por+ x y luego por -3:

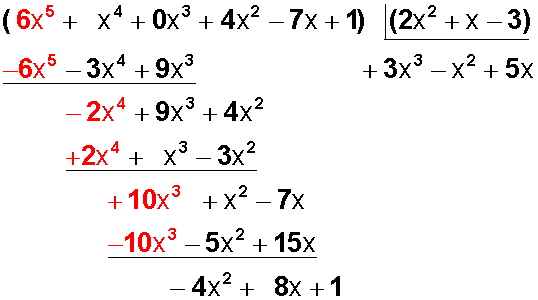
Bajamos el último monomio (+1),

y ahora dividimos -4x 2 : +2x 2 =-2

-2 lo agregamos al cociente y repetimos la operación anterior:

 

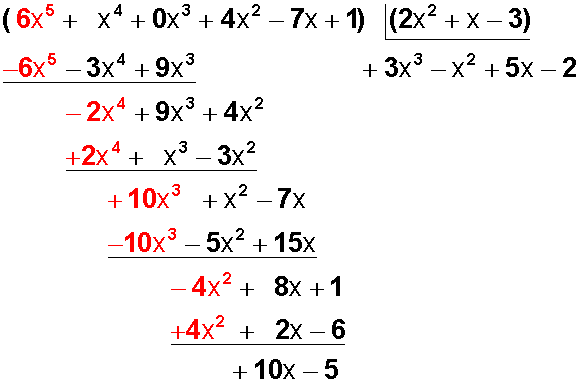
División Sintética

La división sintética es un procedimiento práctico para hallar el cociente y el residuo de la división de un polinomio entero en x por x-a.

Dividamos entre 

Podemos apreciar que el cociente  es un polinomio en x de un grado menor que el del dividendo; que el coeficiente del primer término del cociente es igual al coeficiente del primer término del dividendo y que el residuo es 5.

Sin efectuar la división, el cociente y el residuo pueden hallarse por la siguiente regla práctica:

1)      El cociente de un polinomio en x cuyo grado es 1 menos que el grado del dividendo.

2)      El coeficiente del primer término del cociente es igual al coeficiente del primer término del dividendo.

3)      El coeficiente de un término cualquiera del cociente se obtiene multiplicando el coeficiente del término anterior por el segundo término del binomio divisor, cambiando el signo y sumando este producto con el coeficiente del término que ocupa el mismo lugar  en el dividendo.

4)      El residuo se obtiene multiplicando el coeficiente del último término del divisor, cambiando de signo y sumando este producto con el término independiente del dividendo.

Ejemplo:

Dividamos entre 

Solución:

Dividendo				Divisor
1	-2	-3	+5

Resultado  residuo: 5

Ejemplo:

Efectuar por división sintética 

Solución:

Dividendo	Divisor

Resultado  residuo: 68

Ejemplo:

Efectuar por división sintética 

Solución:

Dividendo	Divisor

Resultado  residuo: 25

Ejemplo:

Efectuar por división sintética  entre 

Solución:

Como este polinomio es incompleto, pues le faltan los términos  y , al escribir los coeficientes ponemos 0 en los lugares que debían ocupar los coeficientes de estos términos.

Dividendo	Divisor

Como el dividendo es de 5° grado, el cociente es de 4° grado los coeficientes del cociente son 1, 4, 0, 0 y -202, el cociente es  y el residuo es -727

COCIENTES NOTABLES

No debe confundirse con Productos notables.

Los cocientes notables son aquellos que resultan de divisiones exactas entre polinomios, es decir que el resto es igual a cero.

${\displaystyle {\frac {(x^{n}\pm y^{n})}{(x\pm y)}}}$

Forma general de un cociente notable

Existen 3 casos de cocientes notables: 

Caso 1 Este caso se produce cuando n es un número par o impar.

 Caso 2 Este caso se produce cuando n es un número par. 

 Caso 3 Este caso se produce cuando n es un número impar.

 Caso 4 (No es un cociente notable) Este caso se produce siendo n un número par o impar, en dicho desarrollo no se genera un cociente notable, ya que posee residuo :