ESTADISTICA:
La estadistica se refiere a un conjunto de metodos,normas,reglas y principios para observar, agrupar,describir,cuantificar y analizar el comportamiento de un grupo
Existe dos tipos de clases de estadisticas.
1.DESCRIPTIVA:Recoge los datos aleatoriamente,los clasifica,representa grafica/y convierte dicha informacion en estadistoca (valores representativos de una poblacion) llamados tambien tendencia central.
2.INFERENCIAL:Maneja el concepto de propabilidad basado en estudios previos de la estadistica descriptivas con el fin de prevesir el comportamiento de una poblacion ante situaciones especificas.
*Los elementos que interveienen en estudio estadistico son primero:
- POBLACION: Es el conjunto de medidas o el reencuentro de todos los elementos que representan una caracteristica comun .El termino poblacion se ussa para denotar el conjunto de elementos el cual se extrae la muestra
MUESTRA : Es un subconjunto de la poblacion de el cual se toman los datos. Se toma una muestra cuando existe algun inpedimiento para someter a una prueba estadistica.Los resultados se asumen para la poblacion ALGUNOS CONCEPTOS BASICOS
CARACTERISTICAS:(caractes ) Correspone a siertos rasgos , cualidades o porpiedades que se poseen los elementos que contienen la poblacion de la muestra. Las caracteristicas de un fenomeno pueden ser : Cualitativas o cuatitativas.
Las caracteristicas cualitativas denominadas tambien atributos son aquelllos que se pueden escribir mediante palabras Por ejemplo, las ventas en valor o cantidad ya sean consurcusales o por dias o por meses ;los empleados de una empresa por cargos;la marca de aceite de un domestico.En los ejemplos anteriores las caracteristicas de cualitativas son: Los nombres de sucursales , dias , meses ,cargos o
marcas
Sucursal
|
Millones
|
Centro
|
220
|
Chapinero
|
80
|
Chico
|
160
|
Lago
|
312
|
Quiroga
|
54
|
Restrepo
|
42
|
Total
|
868
|
Cargo
|
Cantidad
|
Administrador
|
1
|
Celador
|
8
|
Contador
|
2
|
Secretaria
|
3
|
Supervisor
|
5
|
Vendedor
|
36
|
Total
|
55
|
LAS CARACTERISTICAS CUANTITATIVAS Denominadas tambien variables son aquellos sustentibles de ser presesadas unicmanete como la clasificacion de empelados por sueldo o tiempo de servicio; el numero de viajes en el mes realizadas por buses de servicio publicos; el numero de sucursales por volumen de ventas . estas variables se calsifican en discretas incontinua
sera discreta si la variable adimite unicamente valores numericos enteros ; por ejemplo la clasificacion de las fabricas debido al numero de maquinas o empleables
En ellos no se presentan fracciones de maquinas, tales o empleados .
se trta de variable continua se admite valores fraccionales son considerables como tales las empresas de forma de medidas de superficie , peso ,longitud,volumen tiempo ,temperatura,valor.ademas las empresas en medidas de la relacion tales como porcentaje,casas,puntuiaciones.
en la variable continua se valoran intervalos ór lo cual se simplifica su ordenamiento y presentacion
DISTRIBUCION DE FRECUENCIAS
La tabla de frecuencias tiene como finalidad presentar el orden formada los valores que toman las idferentes caracteristicas, en tal forma que permita al lector tener una vision de conjunmto ya sea aclarando el texto del informe o complementando bajo este principio olos datos se clasifican de acuerdo con siertas caracteristicas cualitativas y cuatitativas, inficando el numero de veces que se repite el atributo o la variable.
1. Variables:
para elaborar una tabla de frecuencias ya se para variable discreta o continua se deben tener en cuenta las siguientes simbologias necesarias para el calculo de las diferentes medidas que se aplican n el porcentaje de datos.
2.Variables discretas
Supongamos que se tiene 300 cajas de madera de la bodega de un almacen y cada una de ellas contiene figuras de porcelana se desa examinar las cajas con el fin de saber el numero de figuras que han sufrido on el transporte desde la fabrica hasta la bodega por motivos de tiempo,espacio fisico y personal disponible se toma la decision un 10 % de las cajas por tal razon se tendran 30 cajas de un tal de 300 cajas
N=300 tal poblacion
N=30 Muestra
Cada caja selecciopnada en forma aleatoria se simboliza por xi Donde se inicie para valores desde que esten siendo x 1 , la primera caja seleccionada x2 la segunda y asi sucesivamente.Cada xi Tendra como valor correpondiente de la caracteristica examinada
TEMAS VISTO EL SEGUNDO PERIODO
1 VARIABLE CONTINA
2 HITOGRAMA DE FRECUENCIAS
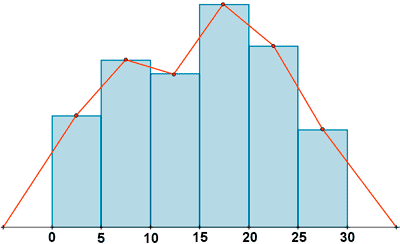
Polígono de frecuencias
TEMAS TRABAJADOS EL SEGUNDO PERIODO
La variable
tabla 5 datos sin agrupar
amplitud de intervalos
taller de recuperacion

Ordenamiento en forma de tabla de los datos estadísticos, asignando a cada dato su frecuenciacorrespondiente. Las Tablas de frecuencias son herramientas de Estadística donde se colocan los datos en columnas representando los distintos valores recogidos en la muestra y las frecuencias(las veces) en que ocurren.








TEMAS TRABAJADOS EL SEGUNDO PERIODO


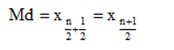

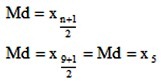
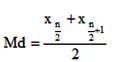

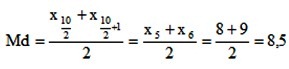
Bimestral 14 de nov 2017
taller 17 de nov 2017

Polígono de frecuencias

TEMAS TRABAJADOS EL SEGUNDO PERIODO
La variable
tabla 5 datos sin agrupar
amplitud de intervalos
taller de recuperacion
Ordenamiento en forma de tabla de los datos estadísticos, asignando a cada dato su frecuenciacorrespondiente. Las Tablas de frecuencias son herramientas de Estadística donde se colocan los datos en columnas representando los distintos valores recogidos en la muestra y las frecuencias(las veces) en que ocurren.

CONSTRUCCIÓN DE LA TABLA DE FRECUENCIAS
- En la primera columna se ordenan de menor a mayor los diferentes valores que tiene la variable en el conjunto de datos.
- En las siguientes columnas (segunda y tercera) se ponen las frecuencias absolutas y las frecuencias absolutas acumuladas.
- Las columnas cuarta y quinta contienen la las frecuencias relativas y las frecuencias relativas acumuladas.
- Adicionalmente (opcional) se pueden incluir dos columnas (sexta y séptima), representando la frecuencia relativa y la frecuencia relativa acumulada como tanto por cien. Estos porcentajes se obtienen multiplicando las dos frecuencias por cien.
Existen cuatro tipos de frecuencias:
Frecuencia absoluta
La frecuencia absoluta (ni) de un valor Xi es el número de veces que el valor está en el conjunto (X1, X2,…, XN).
La suma de las frecuencias absolutas de todos los elementos diferentes del conjunto debe ser el número total de sujetos N. Si el conjunto tiene k números (o categorías) diferentes, entonces:

Frecuencia absoluta acumulada
La frecuencia absoluta acumulada(Ni) de un valor Xi del conjunto (X1, X2,…, XN) es la suma de las frecuencias absolutas de los valores menores o iguales a Xi, es decir:
Frecuencia relativa
La frecuencia relativa (fi) de un valor Xi es la proporción de valores iguales a Xi en el conjunto de datos (X1, X2,…, XN). Es decir, la frecuencia relativa es la frecuencia absoluta dividida por el número total de elementos N:

Las frecuencias relativas son valores entre 0 y 1, 0 ≤ fi ≤ 1. La suma de las frecuencias relativas de todos los sujetos da 1. Supongamos que en el conjunto tenemos k números (o categorías) diferentes, entonces:

Si se multiplica la frecuencia relativa por cien se obtiene el porcentaje (tanto por cien %).
Frecuencia relativa acumulada
Definimos la frecuencia relativa acumulada (Fi) de un valor Xi como la proporción de valores iguales o menores a Xi en el conjunto de datos (X1, X2,…, XN). Es decir, la frecuencia relativa acumulada es la frecuencia absoluta acumulada dividida por el número total de sujetos N:

La frecuencia relativa acumulada de cada valor siempre es mayor que la frecuencia relativa. De hecho, la frecuencia relativa acumulada de un elemento es la suma de las frecuencias relativas de los elementos menores o iguales a él, es decir:
EJEMPLO
Un profesor tiene la lista de las notas en matemáticas de 30 alumnos de su clase. Las notas son las siguientes:

1) Frecuencia absoluta

Se realiza el recuento de la variable que se estudia (notas) para ver el número de veces que aparece cada nota.
Una vez realizado el recuento, se representan las frecuencias absolutas de cada una de las notas (ni). Las frecuencias son: n1(3)=2, n2(4)=4, n3(5)=6, n4(6)=7, n5(7)=5, n6(8)=3, n7(9)=2 y n8(10)=1.
2) Frecuencia absoluta acumulada

Se calculan las frecuencias absolutas acumuladas (Ni) como la suma de las frecuencias absolutas de los valores menores o iguales a Xi:
- N1(3)=n1(3)=2
- N2(4)=n1(3)+n2(4)=2+4=6
- N3(5)=n1(3)+n2(4)+n3(5)=2+4+6=12
- N4(6)=n1(3)+n2(4)+n3(5)+n4(6)=2+4+6+7=19
- N5(7)=n1(3)+n2(4)+n3(5)+n4(6)+n5(7)=2+4+6+7+5=24
- N6(8)=n1(3)+n2(4)+n3(5)+n4(6)+n5(7)+n6(8)=2+4+6+7+5+3=27
- N7(9)=n1(3)+n2(4)+n3(5)+n4(6)+n5(7)+n6(8)+n7(9)=2+4+6+7+5+3+2=29
- N8(10)=n1(3)+n2(4)+n3(5)+n4(6)+n5(7)+n6(8)+n7(9)+n8(10)
- =2+4+6+7+5+3+2+1=30
3) Frecuencia relativa
Se calcula la frecuencia relativa de cada elemento como la división de la frecuencia absoluta entre el total de elementos N=30.
- f1(3) = n1(3)/N = 2/30 = 0,07
- f2(4) = n2(4)/N = 4/30 = 0,13
- f3(5) = n3(5)/N = 6/30 = 0,20
- f4(6) = n4(6)/N = 7/30 = 0,23
- f5(7) = n5(7)/N = 5/30 = 0,17
- f6(8) = n6(8)/N = 3/30 = 0,10
- f7(9) = n7(9)/N = 2/30 = 0,07
- f8(10) = n8(10)/N = 1/30 = 0,03
3.
2. Variables cualitativas[editar]
Son el tipo de variables que como su nombre lo indica expresan distintas cualidades, características o modalidad. Cada modalidad que se presenta se denomina atributo o categoría, y la medición consiste en una clasificación de dichos atributos. Las variables cualitativas pueden ser dicotómicas cuando sólo pueden tomar dos valores posibles, como sí y no, hombre y mujer o ser politómicas cuando pueden adquirir tres o más valores. Dentro de ellas podemos distinguir:
- Variable cualitativa ordinal o variable casi cuantitativa: La variable puede tomar distintos valores ordenados siguiendo una escala establecida, aunque no es necesario que el intervalo entre mediciones sea uniforme, por ejemplo: leve, moderado, fuerte.
- Variable cualitativa nominal: En esta variable los valores no pueden ser sometidos a un criterio de orden, como por ejemplo los colores.
Variables cuantitativas[editar]
Son las variables que toman como argumento cantidades numéricas, son variables matemáticas. Las variables cuantitativas además pueden ser:
- Variable discreta: Es la variable que presenta separaciones o interrupciones en la escala de valores que puede tomar. Estas separaciones o interrupciones indican la ausencia de valores entre los distintos valores específicos que la variable pueda asumir. Ejemplo: El número de hijos (1, 2, 3, 4, 5).
- Variable continua: Es la variable que puede adquirir cualquier valor dentro de un intervalo especificado de valores. Por ejemplo la masa (2,3 kg, 2,4 kg, 2,5 kg,...) o la altura (1,64 m, 1,65 m, 1,66 m,...), o el salario. Solamente se está limitado por la precisión del aparato medidor, en teoría permiten que exista un valor entre dos variables.
) PARA DATOS NO AGRUPADOS
1.1) PARA UN NÚMERO DE DATOS IMPAR
La mediana es el dato que se encuentra a la mitad de la lista. Para calcular su posición se aplica la siguiente ecuación:
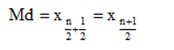
Ejemplo ilustrativo:
Calcular la mediana de las siguientes calificaciones del curso de Estadística evaluadas sobre diez: 10, 8, 6, 4, 9, 7, 10, 9 y 6
Solución:
1) Se ordena los datos de menor a mayor:

2) Se aplica la ecuación:
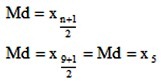
La mediana es el valor de x5 (quinto dato), es decir, Md=8
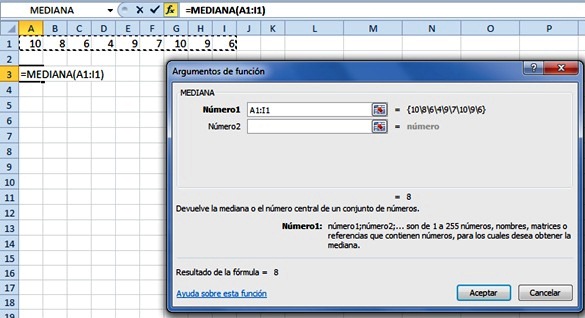
En Excel se calcula así:
Insertar la función MEDIANA(A1:I1) y luego en Aceptar

1.2) PARA UN NÚMERO DE DATOS PAR
La mediana es la media aritmética de los dos datos que se encuentran a la mitad de la lista. Para calcular su posición se aplica la siguiente ecuación:
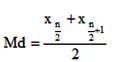
Ejemplo ilustrativo: Calcular la mediana de las siguientes calificaciones del curso de Matemática evaluadas sobre diez: 10, 8, 9, 6, 4, 8, 9, 7, 10 y 9
Solución:
1) Se ordena los datos de menor a mayor:

2) Se aplica la ecuación
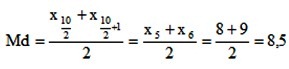
taller 17 de nov 2017
No hay comentarios:
Publicar un comentario